Intelligencia

 

        Létezik egy figyelemre méltó tétel a számítástechnikában, amelyik szerint NAND kapuk összekapcsolásával bármilyen függvényt előállíthatunk. Első látásra ez így elég semmitmondónak tűnhet, pedig a mai tudásunk alapján bátran kijelenthetjük, hogy a függvények képezik az intelligencia alapját, legyen az mesterséges vagy biológiai.

Ha az intelligencia nem más, mint az összetett célok elérésének képessége, akkor rendkívül összetett függvények alkalmazásával olyan struktúrákat hozhatunk létre, amelyek egészen összetett célok elérésére képesek, vagyis intelligensek.

Nos, a megfelelően elrendezett anyag bármilyen összetett függvény kiszámítására képes. Jó példa erre az agyunkban kialakult neurális hálózat, ami úgy néz ki, hogy megfelelően van elrendezve. De arra is van példa, hogy az élettelen anyag van megfelelően elrendezve és számítást végez, lásd a számológépeket. Márpedig a mai számítástechnika alapja a NAND kapu, hiszen csupán NAND kapuk megfelelő kombinálásával bármilyen jól definiált számítást végre lehet hajtani. Elegendő számú NAND kapu elrendezésével tehát olyan eszköz hozható létre, amely bármit ki tud számítani. Ezt az eszközt ma úgy hívjuk, hogy számítógép.

Ilyen megvilágításban, már érdekes lehet, sőt illik közelebbről megvizsgálni a számítógépünk legó-elemét, amelyik a tudatlan anyagból egy egyszerű, ám rendkívüli fontos logikai függvényt fogalmaz meg: a függvény bemenete két bit (legyen A és B), kimenete egy bit (C); 0 logikai állapotú a kimenet, ha mindkét bemenet 1, minden más esetben a kimenet 1 állapotú. A függvény képlete C=/(A*B), vagyis: C egyenlő A ÉS B tagadása – innen származik a függvény neve: Non AND. Ezt a függvény kapjuk például amikor sorba kötünk két kapcsolót egy villanykörtével. A körte csak akkor világít (0), ha mind a két kapcsoló be van kapcsolva, minden más esetben sötét marad (1). Ez a kis apróság az alapja a számítógépünknek, a telefonunknak és bármelyik okos kütyünknek. Nélküle ezek nem léteznének. Olyan fontos, hogy nem árt iderajzolni:

          Persze a mai számítógépekben a NAND kapuk jellemzően miniatűr szilícium lapkára vésett mikroszkopikus tranzisztorokból készülnek és egyre több fér el belőlük ugyanakkora felületen. A következő ábra azt szemlélteti, hogyan lehet NAND kapukkal kifejezni a négy alap logikai függvényt (áramköri legókat): NOT (tagadás), AND (és), OR (vagy), XOR (kizáró vagy: C=/A*B+A*/B). 

Ezekkel az alapáramkörökkel bármilyen logikai függvényt összerakhatunk. Például, egy összeadó áramkört, amelyik három különböző bitet összegez egy kétbites számmá, 11 NAND kapuval lehet megcsinálni:

          Ezt használhatjuk azután két olyan szám összeadására, amelyeket négy biten fejezünk ki, az eredményt pedig értelem szerűen 5 biten kapjuk:

            Látható, hogy ez már egy bonyolultabb függvény, mivel lényegében 44 darab NAND kapuból raktuk össze.

 Végül vegyünk egy olyan függvényt, amelyik két, négy biten kifejezett bináris szám szorzatát számolja ki 8 biten és már van annyira bonyolult, hogy restelljem lerajzolni, hiszen a mai világban elég azt tudni, hogy melyik ikont válasszuk ki és merrefelé forgassuk a telefonunkat, ha le akarunk olvasni egy QR kódot, nem szokás a részletekkel foglalkozni. De hát, ahogy Hofi mondaná, miért pont most változzak meg, hát lerajzolom:

Összesen 164 NAND kaput használtunk. Vessünk rá egy pillantást, azután kapjuk el a tekintetünket, nehogy megigézzen. Hiszen csak egy számítás, egyféle mintázat az anyag tér és időbeli elrendezésében.

Habár a fenti rajzot átlátni egy kihívás, azt mindenképpen szemlélteti, hogy a kézzelfogható fizikai anyag miképpen hozhat létre olyan elvont dolgot, mint az intelligencia. Az csak hab a tortán, hogy a számítás ugyanúgy közegfüggetlen mint az információ. Az anyagot újra, meg újra jobbra cserélhetjük, növelve ezzel a számítások komplexitását, sebességét és nem utolsó sorban a számítások árát.  Ez utóbbival jól állunk, a statisztikák szerint a számítások ára pár évente megfeleződik, eszerint száz év alatt milliószor-milliószor-milliószor csökkent a költsége. Ha az anyag is ennyivel olcsóbbá vált volna, akkor most egy eurócentért megvásárolhatnánk minden árut és szolgáltatást, amit az utóbbi száz évben a Földön létrehoztak.

Most nézzük meg, hogy állunk a sebességgel meg a komplexitással. Habár egy egyszerű számológép is kenterbe ver bennünket egy aritmetikai versenyen, mégsem vagyunk megelégedve, sem a sebességével, sem a komplexitásával. Mert a mai, már klasszikusnak nevezhető számítógépes intelligencia, nem képes az emberi intelligenciához hasonló bonyolult függvények kiszámítására. Ráadásul, minél inkább növeljük a gépi számítások bonyolultságát, annál exponenciálisan több időre és anyagra van szükség ezeket elvégezni.

Ez egy probléma, amin lázasan dolgoztak a kockafejűek az elmúlt évtizedekben. Addig jutottak, hogy eleget tettek Moore törvényének, vagyis menetrend szerűen megduplázták kétévente a klasszikus technológia kapacitását. De ahogy Einstein mondta, egy problémát nem lehet megoldani ugyanazzal a gondolkodásmóddal, amivel létrehoztuk. Ahhoz, hogy radikálisan előbbre jussunk szemlélet kellet váltani.

Az áttörés akkor kezdődött, amikor valakinek támadt egy új ötlete, és tanulmányozni kezdte a biológiai neurális hálózatok számítási képességeit. Egy neurális hálózatot összekapcsolódó neuronok alkotnak, amelyek befolyásolni tudják egymás viselkedését. A neuronok bonyolult elektrokémiai eszközök, különféle részekből, axonokból és dendritekből állnak és rendkívül változatos módon működnek, de van valami közös bennük. Minden neuron átlagosan ezer másikkal áll összeköttetésben, a szinapszisnak nevezett kapcsolatokon keresztül, és ez a durván százbillió szinaptikus kapcsolat, ami az agyban összejön, teszi lehetővé a kiemelkedően összetett feladatok elvégzését és új komplex számítások elsajátítását. A recept egyszerű: a szinapszisok erőssége időnként frissül, a kapcsolatok hol megerősödnek, hol gyengülnek, aszerint, hogy mikor és hogyan aktiválódnak a neuronok. Ezt hívjuk tanulásnak.     

Hamarosan, Heuréka, le is esett a megoldás tantusza. Kockafejűek rájöttek, hogy a tanulás képessége az, ami a mesterséges intelligenciának is a döntően meghatározó feltétele. Innen már csak egy lépés kellett ahhoz, hogy a mesterséges neurális hálózatok modelljét megalkossák. Ebben a modellben minden egyes neuron állapotát és minden egyes szinapszis erősségét egy-egy szám jelöli, lásd az alábbi rajzon.

 Minden neuron rendszeres időközönként frissíti az állapotát. Veszi az összes rákapcsolódó neurontól származó kimenetek átlagát, súlyozza azokat a szinaptikus erősségükkel, opcionálisan konstanst ad hozzá, majd az eredményre alkalmazza az aktivációs függvényt, hogy kiszámítsa a következő állapotot.        

Hát ez elég tudományosan hangzik, de figyeljük meg, hogy lényegében milyen egyszerű dologról van szó. Nézzük meg még egyszer az előbbi rajzot. A kör összeadást végez (átlagol) a bemeneteivel, a vonalak pedig szoroznak (súlyoznak) a rajtuk levő számokkal. A négyzet egy egyszerű függvényt jelent, ami a kör által összegzett értékkel végzi el a számítást.

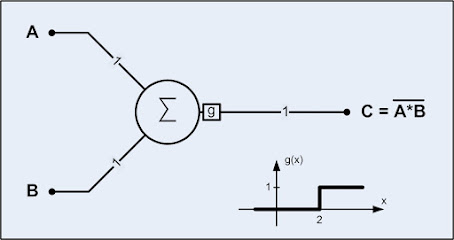
Egyszerű példának vegyük a már annyit emlegetett NAND logikai kaput.  A súlyozó értékek mindkét bemenet esetén 1, az aktiváló függvény pedig egy egyszerű küszöbfüggvény: értéke 1, ha a bemenete nagyobb vagy egyenlő mint 2 és értéke 0, ha a bemenete kisebb mint 2. Ha a neuron bemenetei csak logikai értékeket vehetnek fel (0 vagy 1), akkor a kimenete a NAND logikai függvényt követi.

        Hasonló egyszerű struktúrát szerkeszthetünk a NOT, AND és OR logikai kapura is. Hogy a dolgokat egy kicsit bonyolítsuk nézzük meg egy XOR kapu neuronmodelljét. Ehhez már két rétegű neuronháló szükséges.

Ahhoz, hogy az XOR logikai függvényt (a kimenet csak akkor 1, ha vagy az egyik, vagy a másik bemenet 1) megvalósítsuk, az ábrán látható súlyozásokat használjuk és az összes neuron aktiválási függvénye ugyanaz a g küszöbfüggvény.

És most jön a forradalmi. Ez az egyszerűsített neuronmodell sokkal bonyolultabb dolgok kiszámítására is képes. A következő rajzon látható, hogy mindössze öt neuron miként képes összeszorozni két tetszőleges valós számot, tetszőleges pontossággal. Ehhez csak az szükséges, hogy jól válasszuk meg az aktivációs függvényünket (ebben az esetben ez a rajzon látható szigmoid függvény) és hogy a szinapszisok erősségét (a súlyozó értékeket) frissítsük. Más szóval, beállítjuk a súlyozók pontos értékét, ezáltal betanítjuk a hálózatunkat a feladat elvégzésére.

A tanítás alapgondolata, hogy értékeket adunk a bemenetekre (ezek az un. minták) és a kimeneten mért hiba minimalizálása érdekében módosítjuk a neuronháló súlyait. Ha a hiba pozitív, akkor a háló kimenete túl kicsi, tehát a pozitív bemenetekhez tartozó súlyokat növeljük, a negatívakhoz tartozókat pedig csökkentjük. Ha a hiba negatív, akkor éppen ennek az ellenkezőjét csináljuk. A teljes algoritmus egyesével sorban végig futtatja a mintákat a hálón, és minden egyes példa után a hiba csökkentése érdekében kissé módosítja a súlyokat. A mintahalmaz egyszeri végigfuttatását epoch-nak nevezzük. Az epochokat addig ismételjük, amíg valamilyen leállási feltétel nem teljesül, például amikor a súlyváltozások már nagyon kicsivé válnak. Ez az un. gradiens alapú optimizációs eljárás.

A komplexebb feladatokat - például képfelismerést - ellátó többrétegű (mély) mesterséges neurális hálózatok,  ennél kifinomultabb, izgalmas neveket viselő tanulási szabályokkal állíthatók be; visszaprogramozás (backpropagation), sztochasztikus gradiens lejtő (stochastic gradient), megerősített tanulás (reinforcement learning), meg egyéb más, képtelen elnevezésű algoritmus.

Mindenesetre lenyűgöző, ahogy ezek az egyszerű szabályok alapján definiált neurális hálózatok a kiemelkedően összetett feladatokban képesek emberi szintű teljesítményre, csak azzal, hogy a szinapszisok erősségét jelző számokat egyszerű determinisztikus szabályok alapján megfelelően kiigazítják. Bizonyíthatóan, egy tetszőleges méretű neurális hálózattal elméletben bármi kiszámítható. Ráadásul az eljárás jóval kevesebb neuront igényel, mint amennyi NAND kaput a klasszikus módszer. Ugyebár, két valós tetszőleges nagyságú szám szorzására öt neuront használtunk, míg egy előző példában két, alig négy biten kifejezett bináris szám szorzására 164 NAND kapura volt szükségünk. Egy képfelismerő feladat megoldására pedig nem is lenne elegendő logikai kapunk a mai (még) limitált anyagi platformunkon.

Még mielőtt valaki megjegyezné, hogy jó, jó, de egy NAND kapu létrehozásához elég egy pár alkatrész, nevezetesen két tranzisztor meg egy ellenállás, egy neuronmodell pedig, jóval komplexebb szerkezetű, lássuk be, hogy egy ilyen összehasonlításnak egy anyagi világban van értelme. 

Csakhogy a mai világunkban már nem az anyag a lényeg! A neuronmodell egy anyagon elhelyezett számítás, a számítás ára pedig, mint látjuk, döbbenetes mértékben csökken. Az anyag elrendezhető úgy, hogy miközben engedelmeskedik a fizika meglepően egyszerű törvényeinek, számításokat végez és tanul. Ehhez önmagát kell újrarendeznie, olyan módon, hogy egyre pontosabban tudjon kiszámolni egy kívánt függvényt. Ennek az anyagnak azonban már nem kell biológiainak lennie.